Инструкция

1. Для добавления нового элемента нажмите на нужный, а затем щелкните левой кнопкой мыши на графическом поле.
2. Чтобы соединить элементы, их необходимо предварительно выбрать (один щелчок мыши по каждой вершине), а затем нажать на кнопку Соединить.

Четыре способа ввода данных для калькулятора. Через:

  1. создание схемы логических элементов.
  2. логическую функцию.
  3. карту Карно.
  4. таблицу истинности.

Редактор схемы логических элементов

Сервис представляет собой ряд калькуляторов: создание схемы из логических элементов, построение таблицы истинности по булевой функции (с помощью него можно будет также упростить эту функцию) и редактор карт Карно.
С помощью первой программы можно онлайн создать схему логических элементов. По построенной схеме находятся СКНФ, СДНФ, полином Жегалкина. Имеется возможность минимизировать булеву функцию.
Если схему необходимо построить по заданной таблице истинности, то используйте этот калькулятор (иногда задается просто строка, например, f=10001011).
Количество переменных Стандарт изображений элементов Инверсные входы
INV AND NAND OR NOR XOR MOD IF

Размеры графического полотна

Ширина Высота

Созданную логическую схему можно сохранить в форматах docx и png (меню Действия).

По логической схеме можно построить СКНФ, СДНФ, полином Жегалкина, карты Вейча-Карно, а также минимизировать булеву функцию.
Выводить в отчет:

Проверить на линейность, самодвойственность, монотонность, выяснить существенность переменных

Построение СДНФ

Построение СКНФ

Построение полинома Жегалкина (с помощью треугольника Паскаля и методом неопределенных коэффициентов)

Построение карты Вейча-Карно

Минимизация булевой функции методом Квайна

Упростить функцию через равносильные преобразования

Здесь будет показано решение

Инструкция к сервису

Для добавления логического элемента необходимо выделить его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле.
Чтобы соединить элементы, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить. Для соединения с переменной xi нажмите на соответствующее ей название.
Построенную схему можно сохранить в формате docx или png.

Булевы функции

С помощью этого калькулятора по булевой функции строится таблица истинности, определяются свойства функции и другие параметры (см. вкладку Параметры решения). При этом вводится только само логическое выражение без префикса. Например, при f(x,y,z) = x → y!z, ввести необходимо только x → y!z.
Введеное выражение также можно упростить, используя законы логики высказываний (на следующем шаге выбрать параметр Упростить выражение).

(...) - ввод скобок, x -отрицание (NOT, !, ¬), & - логическое И, AND, ∧, *, v - логическое ИЛИ, OR, ∨, = - эквивалентность, ˜, ≡, ↔, ⊕ - сумма по модулю 2, | - штрих Шеффера, И-НЕ, AND-NOT, ↓ - стрелка Пирса, ИЛИ-НЕ, OR-NOT, ← - обратная импликация.

Для вложенного отрицания необходимо использовать знак !. Например, x v y = !(x v y) или x v y = x v !y

По найденной таблице истинности можно определить логические значения высказываний, например, при x=0, y=0, z=1
Чтобы проверить высказывание на истинность или ложность, функцию необходимо вводить без знака равно (=). Например, A+B→A&B=1, необходимо ввести A+B→A&B. Если в результате преобразований получится, что f=1, то высказывание истинно, если f=0 - ложно.
Проверка справедливости тождества аналитически также проводится в два этапа:упрощается левая, а затем правая части.

Логические (функциональные) элементы {v,&, ¬} являются наиболее распространенными: в силу полноты системы любую булеву функцию (БФ) можно представить в виде суперпозиции дизъюнкции, конъюнкции и отрицания. В качестве функциональных элементов (ФЭ) можно рассматривать любые булевы функции, при этом их можно соединять друг с другом, подавая выходы одних элементов на входы других (суперпозиция БФ).
Область определения БФ E – конечное множество, поэтому БФ можно задать с помощью таблицы истинности, содержащей |E|=2n строк. Столбец значений БФ при этом представляет собой двоичное слово длиной 2n. Поэтому количество различных БФ n переменных равно 22n.
Другие БФ строятся из элементарных с помощью суперпозиций функций.

Основные равносильности логики высказываний

НазваниеФормула
Закон исключенного третьегоX v !X ≡ И
Закон противоречияX & !X ≡ Л
Закон коммутативностиX & Y ≡ Y & X
X v Y ≡ Y v X
Закон ассоциативности(X & Y)&Z ≡ X&(Y&Z)
(X v Y) v Z ≡ X v (Y v Z)
Закон дистрибутивностиX&(Y v Z) ≡ X&Y v X&Z
X v Y&Z ≡ (X v Y)&(X v Z)
Закон двойного отрицания!!X ≡ X
Закон идемпотентностиX&X ≡ X, X v X ≡ X
Законы де Моргана!(X v Y) ≡ !X & !Y
!(X & Y) ≡ !X v !Y
Закон поглощенияX v X&Y ≡ X
X&(X v Y) ≡ X
Законы склеивания(X & Y)v(X & !Y) ≡ X
(X v Y)&(X v !Y) ≡ X
Замена импликацииX → Y ≡ !X v Y
Замена эквиваленцииX = Y ≡ X&Y v !X&!Y
Пример. Упростите выражение: (x˅y˅z)→(x˅y)*(x˅z)
Упростим функцию, используя основные законы логики высказываний.
Замена импликации: A → B = !A v B
Для нашей функции:
(x v y v z)→((x v y) (x v z)) = x v y v z v (x v y) (x v z)
Упростим функцию, используя законы де Моргана: !(A v B) = !A & !B
Для нашей функции:
x v y v z = x y z
По закону дистрибутивности:
(x v y) (x v z) = x v x z v y x v y z
получаем:
f = x y z v x v x z v y x v y z
После элементарных преобразований получаем:
f = x y z v x v x z v y x v y z = x y z v x v y z
f = y z v y z v x

Минимизация булевых функций

В данном сервисе для минимизации булевых функций используются метод Квайна и карт Карно-Вейча. После получения минимальной формы имеется возможность заново построить логическую схему. Если исходная схема понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить).
Сократить БФ можно, применяя некоторые равносильности логики высказываний:
  1. Kx v K ≡ K - тождество поглощения;
  2. Kx v Kx ≡ K - тождество склеивания;
  3. Kx v Ky ≡ K(xvy) - дистрибутивный закон,
где K- элементарная конъюнкция. Большинство методов минимизации БФ основываются на первых двух тождествах. А третье – дистрибутивный закон – уменьшает количество букв в формуле, но выводит формулу из класса ДНФ. При минимизации БФ используют различные термины (и обозначения) для полных элементарных конъюнкций (ПЭК). Наиболее часто используются термины «минтерм» и «конституента единицы». (Для полных элементарных дизъюнкций (ПЭД) используются термины «макстерм» и «конституента нуля»). Слово «конституента» означает «составляющая», а название «минтерм» исходит из определения конъюнкции, как минимального значения ее операндов. При этом используются обозначения mi - для минтерма и Mi - для макстерма. Номер i соответствует двоичной записи той оценки переменных, для которой mi=1.

Метод карт Карно

Склеить можно как целиком всю карту, либо только выделенные единицы (меню Операции).
Количество переменных Сетка

После минимизации можно получить логическую схему функции и построить таблицу истинности (кнопка Далее)

Этот метод используется для БФ не более, чем с шестью аргументами и основан на тождестве склеивания: Kx v Kx ≡ K - две элементарные конъюнкции (ЭК) склеиваются, если они отличаются только знаком инверсии одного аргумента. Чтобы облегчить нахождение таких пар (четверок, восьмерок,…) склеивающихся ЭК, используют специальное представление БФ в виде таблицы – карты Карно (другое название - диаграмма Вейча). Чтобы заполнить карту Карно необходимо щелкнуть левой кнопкой мышки на соответствующую ячейку.
Карта Карно обладает той особенностью, что две ПЭК, соответствующие соседним клеткам карты, отличаются знаком инверсии только одного аргумента, т.е. их можно склеивать. Причем соседними являются не только клетки, например, с номерами 1 и 3, но и клетки с номерами 12 и 8, 12 и 4, т.е. карту можно «сворачивать» в цилиндр, соединяя горизонтальные (вертикальные) ее границы.
Две единицы «склеиваются» каждый раз, когда они стоят рядом в строке или столбце (карту можно свернуть в цилиндр). В результате склеивания число букв, входящих в ПЭК, уменьшается на единицу.

Минимизая функции через равносильные преобразования

см. таблицу равносильных преобразований

Алгоритм минимизии логической функции

  1. Замена импликации и эквиваленции.
  2. Упрощение функции через законы де Моргана.
  3. Раскрытие скобок, используя законы поглощения, исключенного третьего, противоречия.
  4. Минимизация через закон дистрибутивности.

Алгоритм Куайна построения сокращенной ДНФ

  1. Получить СДНФ функции.
  2. Провести все операции неполного склеивания.
  3. Провести все операции поглощения.

Построение логической схемы по таблице истинности

По заданной СДНФ (по таблице истинности) определяются существенные и фиктивные переменные, полином Жегалкина и принадлежность классам T0,T1, S, M, L. Также можно создать новую логическую схему (если не выбран пункт Строить новую схему при минимизации булевой функции). Если вычисления происходят по исходной схеме и она понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить).
Название переменных можно изменить. Для этого их необходимо выбрать (первая строка таблицы).
Количество переменных Ввести как вектор значений (в виде строки)
abcf
000
001
010
011
100
101
110
111
Для установки параметров решения, необходимо нажать Далее.

Пример. Найдите СДНФ(А) и СКНФ(А) с помощью равносильных преобразований и таблицы истинности, если A = xvyv(x→y)&x

Таблица истинности
xyxyxvyxvyx→y(x→y)&xxvyv(x→y)&x
001110100
011010100
100110000
110001111

Упростим функцию, используя основные законы логики высказываний.
Замена импликации
A → B = !A v B
Для нашей функции:
x→y = x v y
f = x v y v (x v y) x
Упростим функцию, используя законы де Моргана онлайн.
!(A v B) = !A & !B
!(A & B) = !A v !B
Для нашей функции:
x v y = x y
f = x y v (x v y) x
По закону дистрибутивности:
x x = 0
(x v y) x = y x
x y v (x v y) x = x y v y x
f = x y
Используя равносильные преобразования, найдем СДНФ(А).
СДНФ(А) = x y
Используя равносильные преобразования, найдем СДНФ(А).
1. Для получения элементарных дизъюнкций используем закон дистрибутивности XvYZ=(XvY)(XvZ).
2. Закон исключенного третьего Xv!X=1. При этом элементарную дизъюнкцию можно отбросить (в силу равносильности C & 1 = C).
3. По закону поглощения XvXYZ = X
A = x y
Из КНФ А путем равносильных преобразований получаем СКНФ А, последовательно добиваясь выполнения четырех свойств СКНФ А.
1. Если элементарная дизъюнкция В, входящая в КНФ А, не содержит переменную xi, тогда заменяем В на Bv(xi & !xi) = (B v xi)(B v !xi)
2. Если в некоторую элементарную дизъюнкцию В переменная xi входит дважды, то лишнюю переменную нужно отбросить, так как xi v xi = xi.
3. Если КНФ А содержит две одинаковых элементарных дизъюнкций, то одну можно отбросить, так как B & B = B
4. Если в элементарную дизъюнкцию входит пара xi v !xi, то ее можно отбросить так как xi v !xi=1, а истинное высказывание из конъюнкции можно выбросить (в силу равносильности C & 1 = C).
A = (x v y y) (y v x x) = (x v y) (x v y) (y v x) (y v x)
A = (x v y) (x v y) (y v x) (y v x)
СКНФ(А) = (x v y) (x v y) (x v y)
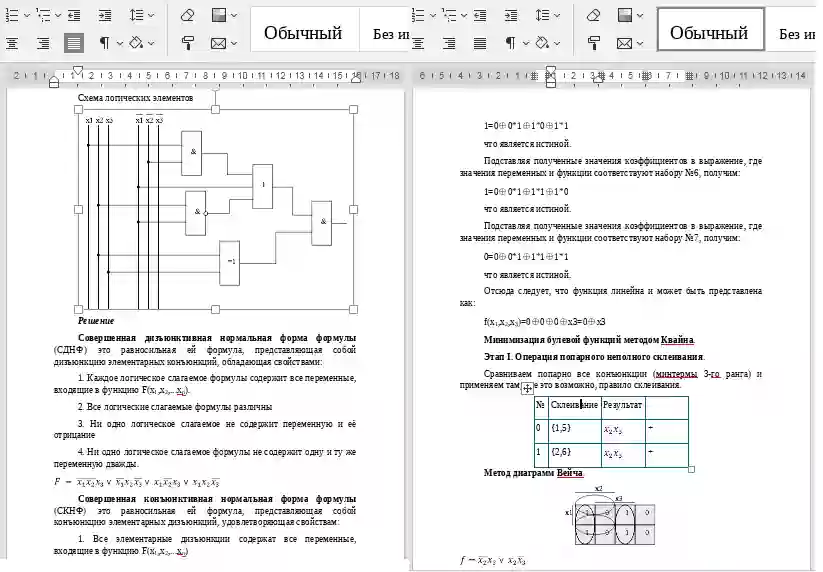
Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами:
1. Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x1,x2,...xn).
2. Все логические слагаемые формулы различны.
3. Ни одно логическое слагаемое не содержит переменную и её отрицание.
4. Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.
F = x y
Совершенная конъюнктивная нормальная форма формулы (СКНФ) это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам:
1. Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x1,x2,...xn).
2. Все элементарные дизъюнкции различны.
3. Каждая элементарная дизъюнкция содержит переменную один раз.
4. Ни одна элементарная дизъюнкция не содержит переменную и её отрицание
F = (x v y) (x v y) (x v y)

Список литературы

  1. Нефедов В.Н., Осипова В.А. Курс дискретной математики. М.,1992.
  2. Бауэр Ф.Л., Гооз Г. Информатика. Вводный курс: Часть 2, М.: Мир, 1990.
  3. Горбатов В.А. Основы дискретной математики. – М.: Высш. школа, 1986. – 312 с.
Задать вопрос или оставить комментарий Помощь в решении Поиск